Thoughts on the Economic Value of Testing
The importance of expanding testing for COVID19 is not really disputed anywhere at the moment. However, testing is largely spoken of as an auxiliary feature of the public health response to the ongoing outbreak; as a tool that informs us where the virus is most prevalent, what measures are or aren't working, etc. Testing may, however, be the most useful public health response in its own right, and as testing rates increase, it may serve as a substitute for broad lockdown measures, rather than merely a complement, enabling us to halt the spread of the virus while throttling less and less of our economy. I thought it might be worth reflecting on just how much a test is actually worth in terms of the economic activity it salvages.
First, how is testing a public health remedy in its own right? This requires a challengeable (but I think still plausible) assumption: that people are, by and large, sufficiently considerate that, when they test positive for the virus, they will voluntarily self-quarantine. Given that assumption, it's easier to understand how ubiquitous testing alone can mitigate the epidemic. If everyone gets tested every day, and everyone who tests positive self-quarantines for two weeks, then everyone else can go on as usual. We have in place, in essence, a lockdown that has 100% sensitivity and 100% specificity. As testing rates increase, both the specificity and the sensitivity of our collective response go up, and the number of 'false positives' (uninfected people forgoing economic activity) declines, so output can go up without increasing the prevalence of the disease. A key point here is that testing isn't just useful in confirming that someone is uninfected and can go back to work, go to restaurants, movies, etc. It's also useful because it reduces the extent to which all the untested people have to reduce their own activity in order for society to achieve the same target R0.
For example, if our target R0 is 1 (basically ensuring stable prevalence), the baseline R0 is 2, the infection prevalence is 0.2, and R0 is proportional to the overall amount of inter-personal interaction going on, then without testing, we must cut back on interaction 1/2 to reach out target. If we test 50% of the population regularly (which might mean daily, weekly, or monthly depending on how certain we want to be), then the 10% of the population that is tested and gets a positive result quarantines, and the remaining 90% can behave as normal, and collectively we have reduced R0 to the same level as in the case where everyone cuts back on interpersonal interaction by 50%. That means that if output is proportional to interpersonal activity (so all transactions require an interpersonal interaction), we can reduce our collective forbearance from 50% to just 10%. In other words, increasing regular testing capacity from 0% to 50% of the population increases output from 50% to 90% of its pre-epidemic level. If pre-crisis per capita GDP per week (we'll assume weekly testing is sufficient) is y and the cost of testing is c, then as long as: 0.5c < 0.4y = c < 0.8y, testing is worth it. Put differently, the societal "profit" from a test is 0.8y - c. So if the average person produces $1,000 worth of value per week, and a test costs $100, the expected surplus of a test is $800 - $100 = $700. A nice 700% profit margin.
Of course, quarantines aren't perfectly effective and not all economic activity requires interpersonal interaction. It may be worth writing out a general formula. First, the parameters: R0_b is the baseline R0, R0_q is the R0 of people in quarantine, .and R0* is our 'target R0.' Next, x, our independent variable, is the fraction of people tested, while R0_adj is the adjusted R0 that the untested people must achieve to reach our target R0:
What this equation is saying, in essence: the first term, 1 - alpha, is the fraction of the economy unaffected by the epidemic; everyone, infected or not, tested or not, contributes this fraction of output the same regardless. The second term, (1 - I)x*A, says that people who test negative produce the same as before the crisis (they produce the full "A" component of their output). Finally, the third term, (1 - x)*A*(1 - F), says that the untested people (1 - x as a fraction of the population) produce at a reduced level, with the vulnerable component of their gross production, A, reduced specifically by a factor of F. The positive testing infected population, of course, doesn't contribute to A at all; they are implicitly counted though as contributing to the fraction of economic activity unaffected by the epidemic (in that they can still work from home and order stuff from Amazon while quarantined) in that the coefficient on the 1 - A term is 1 (i.e., the whole population, including the positives, contributes equally to that fraction of production).
What does this mean in terms of actual numbers? With an infection prevalence of 10%, increasing the fraction of the population tested weekly by 1 percentage point (e.g., from 1% to 2%) salvages 0.45% of our GDP. The US's weekly GDP was about $400 billion, meaning we end up increasing output by roughly $600 per person tested. The use of weekly tests is, of course, somewhat arbitrary; one could do daily tests instead (reducing the value per test to ~$90) or monthly (increasing it to ~$2500). How much one reduces one's interpersonal interactions could be a continuous function of how recently one was tested, but few people are going to invest the mental effort to do that (nor are governments, for that matter, likely to employ tiered lockdowns for people depending the recency of their last negative test), so a rough heuristic is probably most realistic in addition to keeping the math simple.
If we consider the possibility of group testing, the value per test goes up dramatically. With group testing, we can pool potentially dozens of samples, test them all at once, and then if the batch is negative, all individuals have effectively been tested negative. If the batch tests positive, we employ binary optimization to test subgroups within the original group until the infected individual(s) is/are identified. The optimal group size is determined by the prevalence of the infection in the population. For I = 0.1, the optimal group size is 9, and the expected number of people 'deconfined' per test is 3.49, as shown in the following table from a very recent paper by Christian Gollier of the Toulouse School of Economics ("Optimal group testing to exit the covid confinement"), linked below.
Gollier, as it happens, also estimates the economic value per test, as you can see. His estimates are derived from using the two-month per capita GDP of the EU (assuming each test deconfines a worker for two months). Since Euros are only slightly more valuable than dollars these days, he reaches a value of about $19,000 per test at I = 0.1. Since optimized group testing deconfines roughly 4x as many people as individual tests, my estimate, if the frequency of tests were reduced to every two months (obviously, the if you're tested every week, each test can only be said to increase your earnings due to deconfinement by one weeks worth) we end up with a value $600*4*9 (2 months = 9 weeks roughly) = $21,600. Since the per capita GDP of the US is almost twice that of the EU, we should get a number of about $36,000, though I'm also assuming that roughly half of output can survive quarantine (e.g., people like me who can pretend to work from home while really blogging). There also two other additional factors in my rudimentary analysis: 1) I assume that the alternative to being tested is not full quarantine but only partial quarantine (since I'm assuming the goal is merely to reduce R0 to about 0.9); and 2) I assume even untested people produce/earn more when the testing rate increases since they can afford to self-isolate less while keeping R0 the same, due to the increase in the fraction of positives who are identified and fully quarantined. Those factors, of course, go in opposite directions. Overall, I'm fairly pleased with the coherence between my makeshift model and Collier's estimates.
The general takeaway: under an optimized group testing regime, the value of a test is probably over $2,000 and potentially as high as $20,000, depending on the frequency of testing. What's the cost of a test? At Everlywell, the test is $135. Al-Jazeera however reports that a rapid test may soon be available in the UK and Senegal for only $1. The former, of course, is more realistic, but over time the costs are likely to fall rapidly. Even at $135, it is clearly worth it. There are other costs worth considering, of course. Mass testing on the scale I'm describing (currently the US tests around 100,000 people per day in the US, or fewer than a million per week; I'm talking about increasing that by about two orders of magnitude or so or more) would require a lot of labor, perhaps hundreds of thousands of personnel swabbing people at workplaces, schools, and mass testing stations all over the country. Of course, if we assume it's possible to collect, say, a test a minute, even if testing personnel make an average of $60 an hour (a six figure salary) it would only add 1$ per test. There would be administrative costs, transportation costs, the cost of actually running the test, and the cost of people having to take a few minutes a week to be swabbed, but overall, it seems reasonable that the total cost per test could be brought under $200, and potentially much lower.
My expectation and hope, therefore, is that, after the current outbreak is over, when COVID19 continues to be a chronic issue for society as we await the release of vaccines and new treatments, our principle goal, and perhaps the greatest entrepeneurial opportunity of our time, will be to expand the availability, increase the rapidity, and reduce the costs of testing to the point where it becomes ubiquitous and mundane. This seems to be doable. Even if we've only accomplished about 1% of it so far, we've managed that in the span of a few weeks and under the burden of crippling overregulation. We've begun to solve the latter problem somewhat, and other countries no wealthier than the US have expanded testing capacity many times as much as we have. Though my parameter values are admittedly rather speculative, I think the numbers suggest that our primary focus for the medium and long term should be the achievement of massive everyday testing. This development would allow us to salvage the vast majority of the economic losses we would otherwise suffer under lockdowns and stay-at-home orders without impeding our ability to drive down the prevalence of the virus, and would allow a return to a relatively normal life without incurring major inconvenience or crippling costs to society.
Citations:
Gollier, Christian, "Optimal group testing to exit the covid confinement." Available at: https://www.tse-fr.eu/sites/default/files/TSE/documents/doc/by/gollier/group_testing.pdf
Everlywell test cost: https://www.pennlive.com/news/2020/03/coronavirus-home-test-kits-are-coming-out-monday-heres-how-to-get-one-the-cost-and-more.html
$1 test: https://www.aljazeera.com/news/2020/03/senegal-10-minute-coronavirus-test-1-200327053901231.html
First, how is testing a public health remedy in its own right? This requires a challengeable (but I think still plausible) assumption: that people are, by and large, sufficiently considerate that, when they test positive for the virus, they will voluntarily self-quarantine. Given that assumption, it's easier to understand how ubiquitous testing alone can mitigate the epidemic. If everyone gets tested every day, and everyone who tests positive self-quarantines for two weeks, then everyone else can go on as usual. We have in place, in essence, a lockdown that has 100% sensitivity and 100% specificity. As testing rates increase, both the specificity and the sensitivity of our collective response go up, and the number of 'false positives' (uninfected people forgoing economic activity) declines, so output can go up without increasing the prevalence of the disease. A key point here is that testing isn't just useful in confirming that someone is uninfected and can go back to work, go to restaurants, movies, etc. It's also useful because it reduces the extent to which all the untested people have to reduce their own activity in order for society to achieve the same target R0.
For example, if our target R0 is 1 (basically ensuring stable prevalence), the baseline R0 is 2, the infection prevalence is 0.2, and R0 is proportional to the overall amount of inter-personal interaction going on, then without testing, we must cut back on interaction 1/2 to reach out target. If we test 50% of the population regularly (which might mean daily, weekly, or monthly depending on how certain we want to be), then the 10% of the population that is tested and gets a positive result quarantines, and the remaining 90% can behave as normal, and collectively we have reduced R0 to the same level as in the case where everyone cuts back on interpersonal interaction by 50%. That means that if output is proportional to interpersonal activity (so all transactions require an interpersonal interaction), we can reduce our collective forbearance from 50% to just 10%. In other words, increasing regular testing capacity from 0% to 50% of the population increases output from 50% to 90% of its pre-epidemic level. If pre-crisis per capita GDP per week (we'll assume weekly testing is sufficient) is y and the cost of testing is c, then as long as: 0.5c < 0.4y = c < 0.8y, testing is worth it. Put differently, the societal "profit" from a test is 0.8y - c. So if the average person produces $1,000 worth of value per week, and a test costs $100, the expected surplus of a test is $800 - $100 = $700. A nice 700% profit margin.
Of course, quarantines aren't perfectly effective and not all economic activity requires interpersonal interaction. It may be worth writing out a general formula. First, the parameters: R0_b is the baseline R0, R0_q is the R0 of people in quarantine, .and R0* is our 'target R0.' Next, x, our independent variable, is the fraction of people tested, while R0_adj is the adjusted R0 that the untested people must achieve to reach our target R0:
R0_adj = R0* - x*R0_q)/(1 - x)
From here, we can infer the necessary level of social forbearance, F:
F = (R0_b - R0_adj)/(R0_b - R0_q)
Finally, if we have parameter A = the fraction of the economy susceptible to lockdowns, etc. (where a total lockdown would reduce output by A) and I = the infected fraction of the population, then economic output (as a fraction of pre-crisis output) obtainable while keeping R0 constant, written as a function of testing fraction x is:
y = (1 - A) + (1 - I)x*A + (1 - x)*A*(1 - F)
What this equation is saying, in essence: the first term, 1 - alpha, is the fraction of the economy unaffected by the epidemic; everyone, infected or not, tested or not, contributes this fraction of output the same regardless. The second term, (1 - I)x*A, says that people who test negative produce the same as before the crisis (they produce the full "A" component of their output). Finally, the third term, (1 - x)*A*(1 - F), says that the untested people (1 - x as a fraction of the population) produce at a reduced level, with the vulnerable component of their gross production, A, reduced specifically by a factor of F. The positive testing infected population, of course, doesn't contribute to A at all; they are implicitly counted though as contributing to the fraction of economic activity unaffected by the epidemic (in that they can still work from home and order stuff from Amazon while quarantined) in that the coefficient on the 1 - A term is 1 (i.e., the whole population, including the positives, contributes equally to that fraction of production).
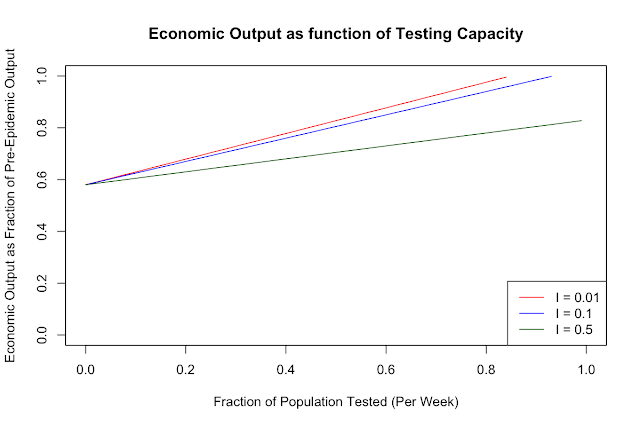
What does this look like if we pick some plausible enough sounding parameter values out of the air? Let's suppose A = 0.5 (so, 50% of the economy is vulnerable to the epidemic). Since it's estimated that employment and output will fall by about 30% or so this quarter, and a sizable minority of the 'social economy' (grocery stores, pharmacies, etc.) is still operational, I thought 50% was a reasonable number. For the others: R0_b = 3; R0_q = 0.5 (so, quarantined people still have an R0 of 0.5). This parameter makes the model a little more robust to my key assumption: one can think of this as also taking into account a measure of non-compliance with self-quarantine norms . R0* - our target R0 - is 0.9, so the we are on a trajectory toward eliminating the virus from the population. Finally, for the infection prevalence, I, I will consider values of 0.01, 0.1, and 0.5, since this is the parameter that is most important in determining the slope, or the returns to more testing. Here's what the plots of output (again, as a fraction of original output) against fraction of the population tested regularly look like:
For intuitive reasons, as the infection prevalence goes up, the value of testing goes down: if the vast majority of the population has the virus, then testing doesn't increase output much, since few people test negative and get the go ahead to live normally, and most of the population has to keep quarantining anyway to keep R0 down. The slopes for I = 0.01, 0.1, and 0.5 are: 0.495, 0.45, and 0.25, respectively. The marginal value of testing when 50% of the population is infected is only about hald what it is when only 1% is infected. This of course highlights the importance of widespread testing early in an epidemic, when it is most valuable.
What does this mean in terms of actual numbers? With an infection prevalence of 10%, increasing the fraction of the population tested weekly by 1 percentage point (e.g., from 1% to 2%) salvages 0.45% of our GDP. The US's weekly GDP was about $400 billion, meaning we end up increasing output by roughly $600 per person tested. The use of weekly tests is, of course, somewhat arbitrary; one could do daily tests instead (reducing the value per test to ~$90) or monthly (increasing it to ~$2500). How much one reduces one's interpersonal interactions could be a continuous function of how recently one was tested, but few people are going to invest the mental effort to do that (nor are governments, for that matter, likely to employ tiered lockdowns for people depending the recency of their last negative test), so a rough heuristic is probably most realistic in addition to keeping the math simple.
If we consider the possibility of group testing, the value per test goes up dramatically. With group testing, we can pool potentially dozens of samples, test them all at once, and then if the batch is negative, all individuals have effectively been tested negative. If the batch tests positive, we employ binary optimization to test subgroups within the original group until the infected individual(s) is/are identified. The optimal group size is determined by the prevalence of the infection in the population. For I = 0.1, the optimal group size is 9, and the expected number of people 'deconfined' per test is 3.49, as shown in the following table from a very recent paper by Christian Gollier of the Toulouse School of Economics ("Optimal group testing to exit the covid confinement"), linked below.
prevalence
|
optimal group
|
expected number
|
expected benefit
|
ratio (p)
|
size (n)
|
deconfined per test (N)
|
of test (qN)
|
0.01
|
99
|
36.60
|
189 129 €
|
0.05
|
19
|
7.17
|
37 046 €
|
0.1
|
9
|
3.49
|
18 016 €
|
0.2
|
4
|
1.64
|
8 466 €
|
0.3
|
3
|
1.03
|
5 317 €
|
0.4
|
2
|
0.72
|
3 720 €
|
Gollier, as it happens, also estimates the economic value per test, as you can see. His estimates are derived from using the two-month per capita GDP of the EU (assuming each test deconfines a worker for two months). Since Euros are only slightly more valuable than dollars these days, he reaches a value of about $19,000 per test at I = 0.1. Since optimized group testing deconfines roughly 4x as many people as individual tests, my estimate, if the frequency of tests were reduced to every two months (obviously, the if you're tested every week, each test can only be said to increase your earnings due to deconfinement by one weeks worth) we end up with a value $600*4*9 (2 months = 9 weeks roughly) = $21,600. Since the per capita GDP of the US is almost twice that of the EU, we should get a number of about $36,000, though I'm also assuming that roughly half of output can survive quarantine (e.g., people like me who can pretend to work from home while really blogging). There also two other additional factors in my rudimentary analysis: 1) I assume that the alternative to being tested is not full quarantine but only partial quarantine (since I'm assuming the goal is merely to reduce R0 to about 0.9); and 2) I assume even untested people produce/earn more when the testing rate increases since they can afford to self-isolate less while keeping R0 the same, due to the increase in the fraction of positives who are identified and fully quarantined. Those factors, of course, go in opposite directions. Overall, I'm fairly pleased with the coherence between my makeshift model and Collier's estimates.
The general takeaway: under an optimized group testing regime, the value of a test is probably over $2,000 and potentially as high as $20,000, depending on the frequency of testing. What's the cost of a test? At Everlywell, the test is $135. Al-Jazeera however reports that a rapid test may soon be available in the UK and Senegal for only $1. The former, of course, is more realistic, but over time the costs are likely to fall rapidly. Even at $135, it is clearly worth it. There are other costs worth considering, of course. Mass testing on the scale I'm describing (currently the US tests around 100,000 people per day in the US, or fewer than a million per week; I'm talking about increasing that by about two orders of magnitude or so or more) would require a lot of labor, perhaps hundreds of thousands of personnel swabbing people at workplaces, schools, and mass testing stations all over the country. Of course, if we assume it's possible to collect, say, a test a minute, even if testing personnel make an average of $60 an hour (a six figure salary) it would only add 1$ per test. There would be administrative costs, transportation costs, the cost of actually running the test, and the cost of people having to take a few minutes a week to be swabbed, but overall, it seems reasonable that the total cost per test could be brought under $200, and potentially much lower.
My expectation and hope, therefore, is that, after the current outbreak is over, when COVID19 continues to be a chronic issue for society as we await the release of vaccines and new treatments, our principle goal, and perhaps the greatest entrepeneurial opportunity of our time, will be to expand the availability, increase the rapidity, and reduce the costs of testing to the point where it becomes ubiquitous and mundane. This seems to be doable. Even if we've only accomplished about 1% of it so far, we've managed that in the span of a few weeks and under the burden of crippling overregulation. We've begun to solve the latter problem somewhat, and other countries no wealthier than the US have expanded testing capacity many times as much as we have. Though my parameter values are admittedly rather speculative, I think the numbers suggest that our primary focus for the medium and long term should be the achievement of massive everyday testing. This development would allow us to salvage the vast majority of the economic losses we would otherwise suffer under lockdowns and stay-at-home orders without impeding our ability to drive down the prevalence of the virus, and would allow a return to a relatively normal life without incurring major inconvenience or crippling costs to society.
Citations:
Gollier, Christian, "Optimal group testing to exit the covid confinement." Available at: https://www.tse-fr.eu/sites/default/files/TSE/documents/doc/by/gollier/group_testing.pdf
Everlywell test cost: https://www.pennlive.com/news/2020/03/coronavirus-home-test-kits-are-coming-out-monday-heres-how-to-get-one-the-cost-and-more.html
$1 test: https://www.aljazeera.com/news/2020/03/senegal-10-minute-coronavirus-test-1-200327053901231.html
Comments
Post a Comment